Today we learnt more about the 4 methods to figure out sequences and series.
Shodor- There is a link www.shodor.org/interactive/activities/Sequencer where you can put in your information from the question and it shows you the graph, and gives you the number values below the graph
Sequence mode-You turn your calculator's mode to Sequence. You can fill in the y=, set the window, see the graph, see the table
Wednesday, September 30, 2009
Tuesday, September 29, 2009
"Sequences & Series
This unit is split into two parts:
1)Geometric/Arithmetic sequences and prediction, stability, exponential growth.
2)Fractal(self similarity-reduced size of the whole, split) Analysis
Fractal-Sierpinski has examples(triangle and square)
There are 4 methods to solving these problems. Mr. Max gave us the first two, and for homework we were to find the other 2.
1)Geometric/Arithmetic sequences and prediction, stability, exponential growth.
2)Fractal(self similarity-reduced size of the whole, split) Analysis
Fractal-Sierpinski has examples(triangle and square)
There are 4 methods to solving these problems. Mr. Max gave us the first two, and for homework we were to find the other 2.
1-Calculator Home Screen Method
2-Excel(making a chart with answers and another with formulas)
3-Sequence mode on the calculator
4-Shodor
Matrix Modelling is over!
On Friday we were supposed to write our test, but at the start of class we found out we had an assembly to say that the Swan Valley is going to host the 2012 Manitoba Summer Games. When we got back from the assembly we had a choice to write the first half of the test or study, and yesterday we finished writing the test.
Thursday, September 24, 2009
Matrix Modelling Review
Today we started off the class with our review. Mr.Max divided the unit into 4 parts:
1)Matrix Info-vocab, naming, calcuators, matrix operations(+,-,scalar X, matrix X)
2)Matrix Multiplication in context(fast, avoiding nonsense calculations), word problems
3)Transition Matricies-RowXSquare, [B]X[A]^n(stability), loopies, decimals in matrices, 1 sum(each row=1)
4)Networks-Directed(node, direct route, at most, exactly) and Non-Directed(two-way)
We then went over some provincial exam questions from previous exams for some more review. For the test tomorrow we are allowed to bring a 8.5X11 formula sheet.
1)Matrix Info-vocab, naming, calcuators, matrix operations(+,-,scalar X, matrix X)
2)Matrix Multiplication in context(fast, avoiding nonsense calculations), word problems
3)Transition Matricies-RowXSquare, [B]X[A]^n(stability), loopies, decimals in matrices, 1 sum(each row=1)
4)Networks-Directed(node, direct route, at most, exactly) and Non-Directed(two-way)
We then went over some provincial exam questions from previous exams for some more review. For the test tomorrow we are allowed to bring a 8.5X11 formula sheet.
Wednesday, September 23, 2009
Directed Networks
Today we started class with Mental Math, and went over a question that was for homework yesterday. Also, there was a big conversation on homework being due, and if a person doesn't get their homework done the first day, it can be made up when they have the chance.
With Direct & Indirect networks:
Matrix A^1=direct-1 leg stop
Matrix A^2=indirect-through exactly 1 node
Matrix A^3=indirect-through exactly 2 nodes(2 stops before reaching the destination)
Directed Networks:
If the question asks you for the number of ways each point can get back to itself using no more than "x" relays, you have to make all the matricies you can. The first matrix is direct connections, the second is through one relay, ect until you reach the total numbers of nodes you can go through. Once you have made all the matrices you can, add them together and you will get the total number of node to itself connections through AT MOST "x" relays.
For the remainder of class we are to look at old provincial exams and do some questions from them for practice, and as a study tool for the test on Friday.
With Direct & Indirect networks:
Matrix A^1=direct-1 leg stop
Matrix A^2=indirect-through exactly 1 node
Matrix A^3=indirect-through exactly 2 nodes(2 stops before reaching the destination)
Directed Networks:
If the question asks you for the number of ways each point can get back to itself using no more than "x" relays, you have to make all the matricies you can. The first matrix is direct connections, the second is through one relay, ect until you reach the total numbers of nodes you can go through. Once you have made all the matrices you can, add them together and you will get the total number of node to itself connections through AT MOST "x" relays.
For the remainder of class we are to look at old provincial exams and do some questions from them for practice, and as a study tool for the test on Friday.
Tuesday, September 22, 2009
Networks & Matricies
Today we learnt about Directed(one-way streets) and Non-Directed networks(two-way streets). To do so, we started with a diagram that had routes to the nodes. We had to figure out how many ways we could get from one place to the next either directly, or indirectly(through another node). After we did this for a half hour, Mr.Max showed us how to do it easily on the calculator by taking the direct route matrix and squaring it to get to the second matrix that was from one place to another through one other node.
Monday, September 21, 2009
Transition Matricies
Today we went over one of our homework questions on transition matrices. To continue to the "next transition" you first multiply the row by the square, and to continue you multiply the resulting matrix by the original and can continue pushing enter to see the next matrix.
There is now a link on the class blog to previous provincial math exams. And we also have a test on Friday.
There is now a link on the class blog to previous provincial math exams. And we also have a test on Friday.
Friday, September 18, 2009
Transition Matricies
A transition matricies question has the info moving around(students changing their minds over what restaruaunt they prefer). There is a chart showing what people stay at which restaraunt, and what ones they switch to.
The first step is to create a nXn matrix using decimal equivalents to show the switches and input them in the calculator. Headers for the rows and columns are very important to keep track of.
The second step is to create a row matrix with either A)Real # values or B) the % of some distribution, which is also put in the calculator.
The third and final step is to multiply the row matrix by the nXn matrix which gives you the answer of the next transition. This can be continued until stability is reached. To prove stability you can do the transition to the power of 50, then 51 to see if any digits change.
The first step is to create a nXn matrix using decimal equivalents to show the switches and input them in the calculator. Headers for the rows and columns are very important to keep track of.
The second step is to create a row matrix with either A)Real # values or B) the % of some distribution, which is also put in the calculator.
The third and final step is to multiply the row matrix by the nXn matrix which gives you the answer of the next transition. This can be continued until stability is reached. To prove stability you can do the transition to the power of 50, then 51 to see if any digits change.
Matrix Multiplication Question
We were given a question yesterday to do with matrix multiplication and were asked to post our thoughts through it on our blogs to look at in the future.
There are 3 factories of type A that makes 30 kitchens each week and 40 bathrooms, as well as 8 factories of type B with 10 kitchens each week and 15 bathrooms. This information could be made into a 2X2 matrix with row headers "Kitchen" & "Bathroom" and column headers factories"A" &"B". The first part of the question asked for total weekly production of both suites from both kinds of factories. To do so, the 2X2 matrix had to by multiplied by a 2X1 matrix so the inside numbers were the same. 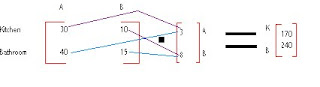 The next part of the question was to find the market value of all suites per week. To do this, the total of each suite had to be multiplied by the total value of each suite. The 2X1 had to be multiplied by a 1X2 matrix with values to work, resulting in a 1X1 matrix with the total value of the goods purchased
The next part of the question was to find the market value of all suites per week. To do this, the total of each suite had to be multiplied by the total value of each suite. The 2X1 had to be multiplied by a 1X2 matrix with values to work, resulting in a 1X1 matrix with the total value of the goods purchased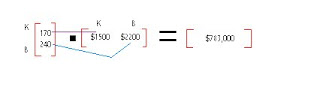
 The next part of the question was to find the market value of all suites per week. To do this, the total of each suite had to be multiplied by the total value of each suite. The 2X1 had to be multiplied by a 1X2 matrix with values to work, resulting in a 1X1 matrix with the total value of the goods purchased
The next part of the question was to find the market value of all suites per week. To do this, the total of each suite had to be multiplied by the total value of each suite. The 2X1 had to be multiplied by a 1X2 matrix with values to work, resulting in a 1X1 matrix with the total value of the goods purchased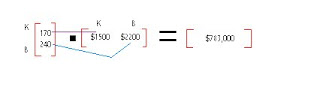
Thursday, September 17, 2009
Two-Finger Method
The two finger method is used for Matrix Multiplication. To form it, the left hand is a thumbs up with the index finger pointing to the right, and the right hand forms a backwards "L".
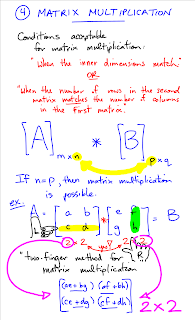

The right hand uses all columns up before the left hand moves to the next row. Each row & column's product is an element in the resulting matrix.
Tuesday, September 15, 2009
First Few Days of Class-Matrix Modelling
Sept 14th 2009:
The third and forth parts to matrices are "Scalar" multiplication(matrix multiplied by a scalar quantity measure), and "Matrix" multiplication. Matrix multiplication can only be done
Sept 11th 2009:
On the second day of class we were taught about Matrix Modelling. Every matrix has Rows&Columns(listed in this order) and the numbers in each is an element. The first 2 parts to Matrices are addition and subtraction, which cannot be done unless they have the same number of rows and columns. To do so, thinking of the numbers overlapped will allow you to see the end result.
The third and forth parts to matrices are "Scalar" multiplication(matrix multiplied by a scalar quantity measure), and "Matrix" multiplication. Matrix multiplication can only be done
when the inner dimensions match
or
the # of rows in the 2nd matrix matches the # of columns in the 1st matrix
*This is where the "Two-Finger Method" is used*
Sept 11th 2009:
On the second day of class we were taught about Matrix Modelling. Every matrix has Rows&Columns(listed in this order) and the numbers in each is an element. The first 2 parts to Matrices are addition and subtraction, which cannot be done unless they have the same number of rows and columns. To do so, thinking of the numbers overlapped will allow you to see the end result.
Goals!
Specific
Measurable
Attainable
Realistic
Timely
Goals:
~To acheive marks of 80% or higher in the remainder of my High School courses
~To decide on a career that I will enjoy that allows me to help others within the next 3 months
~To be accepted to UofM or UofW
~To not rely on my parents for more money than already put aside for my education
~To be a good role model for my younger siblings and try to help them make smart choices
Measurable
Attainable
Realistic
Timely
Goals:
~To acheive marks of 80% or higher in the remainder of my High School courses
~To decide on a career that I will enjoy that allows me to help others within the next 3 months
~To be accepted to UofM or UofW
~To not rely on my parents for more money than already put aside for my education
~To be a good role model for my younger siblings and try to help them make smart choices
Subscribe to:
Comments (Atom)